《抛物线及其标准方程》教学设计
来源:柳州市第二中学 作者: 简璐 已有0人评论 2018/1/4 21:24:23
加入收藏

柳州市第二中学 简璐
课题:抛物线及其标准方程
教材:普通高中课程标准实验教科书 数学选修2-1(人教A版) 高二年级
一、教学目标和重点难点
遵循《普通高中数学课程标准》对本节的教学要求,我将这节课的教学目标、重
点和难点设置为:
教学目标:
1.经历从具体情景中抽象出抛物线几何特征的过程;
2.掌握抛物线的几何图形,定义和标准方程;
3.进一步巩固圆锥曲线的研究方法,体会类比法,直接法和数形结合思想在数学中的应用;
4.感受抛物线的广泛应用和文化价值,体会学习数学的乐趣和数学美.
教学重点:
1.掌握抛物线的定义和相关概念;
2. 掌握抛物线的标准方程.
教学难点:
1.让学生从抛物线的画法中抽象概括出抛物线的定义。
2.选择恰当的坐标系,推导抛物线的方程,比较得出抛物线的标准方程。
二、教学问题诊断
本节课的第一个教学难点是从抛物线的画法中抽象概括出抛物线的定义,对教学难点的突破我采取的策略是:
1.类比学习椭圆,双曲线的过程和方法去学习抛物线。
2.学生在抽象概括抛物线定义时,容易忽略抛物线定义中“点F不在直线上”这个条件,为了加深学生对这个条件的理解,教学中通过师生互动来引导学生逐步完善抛物线的定义,并以小组合作交流的方式讨论这个条件的必要性。
本节课的第二个教学难点是对比得到抛物线的标准方程。我将依据学生的认知习惯,激励学生分小组活动——推导抛物线的方程,采取如下策略:
1.坐标系的建立——教师不作引导,由学生自己选择建系方式,再将学生的结果用投影仪展示出来,并进行归纳.
2.求抛物线的方程——全班学生分工,求出不同建系方式下的抛物线方程通过比较,明确第2种建系方式所得的抛物线方程最简洁,并把这个方程叫做抛物线的标准方程.
3.明确抛物线标准方程的四种形式——给出问题5,先让学生独立思考,再组织学生以小组的方式进行讨论,以加深学生对抛物线标准方程的理解。
三、教学过程
教学过程 | 设计说明 |
一、 课堂导入 1. 生活中的抛物线: (1) 投篮时篮球的运行轨迹是抛物线; (2) 广西柳州文惠桥的桥拱的形状是抛物线; (3) 卫星天线是根据抛物线的原理制造的. 2. 数学中的抛物线: 一元二次函数的图像是一条抛物线. 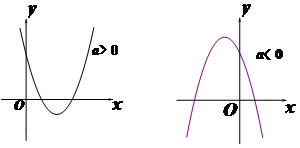
提出问题:为什么一元二次函数的图像是一条抛物线? | 通过生活中的抛物线使学生认识到学习抛物线的必要性。 通过问题引导引发学生的认知冲突,激发学生的学习欲望。 |
二、 抛物线的定义 1. 抛物线的画法 (1) 给出作图步骤. 第1步:取定点F和一条不过点F的定直线l; 第2步:在直线l上任取一点H,过H作; 第3步:作线段FH的垂直平分线m,直线m与MH交于点M。 (2) 用几何画板展示作图过程. 问题1:拖动点H,观察点M的轨迹,点M满足的几何条件是什么? (3) 结论 动点M满足的几何条件是:动点M到定点F的距离等于它到定直线l的距离。 2. 抛物线的定义 问题2:你能给抛物线下个定义吗? 抛物线的定义:平面内与一个定点F和一条定直线l(l不过F)的距离相等的点的轨迹叫作抛物线。 问题3:为什么定点F不能在定直线l上?若点F在直线l上,则轨迹为定点F垂直于直线l的直线 . . 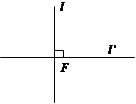
3. 抛物线的相关概念: 定点F:抛物线的焦点. 定直线l:抛物线的准线. 设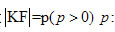 焦点到准线的距离. 焦点到准线的距离. (以上归纳为“三定”,方便记忆) 抛物线的对称轴与抛物线的交点O:抛物线的顶点 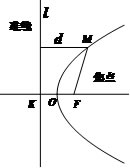
4. 抛物线的定义的应用. 观察下图,过点F并且和直线l相切的圆的圆心所形成的轨迹是什 么?并做出合理解释。(用几何画板演示) 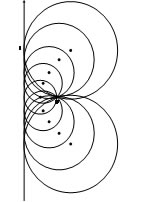
| 抛物线的画法比较复杂,让学生自己画抛物线,操作起来很困难,学生很难完成.因此我运用几何画板来演示画抛物线的过程. 加深学生对抛物线定义中的条件“l不过F”的理解. 目的是对抛物线定义的应用,同时也给出了课堂导入时所给的问题的一种解决方法. |
三、
抛物线的方程 1. 方程推导 (1) 建系 请同学们将抛物线画在草稿纸上, 自己建立平面直角坐标系。 (2) 推导 问题4:以下三种建系方式,你认为哪种建系方式最好?请说明理由,并且推导出抛物线的方程。 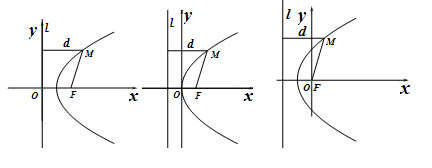
提示:设 ,先将抛物线的焦点坐标和准线方程求出来,再来求抛物线的方程。 ,先将抛物线的焦点坐标和准线方程求出来,再来求抛物线的方程。 三种建系方式下的抛物线方程分别为: , , , , .不难得出,第二种建系方式下的抛物线方程最简洁,因此第二种建系方式最好。 .不难得出,第二种建系方式下的抛物线方程最简洁,因此第二种建系方式最好。 2. 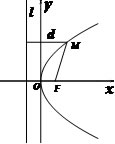 抛物线的标准方程: 抛物线的标准方程:
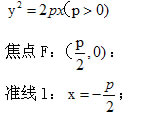
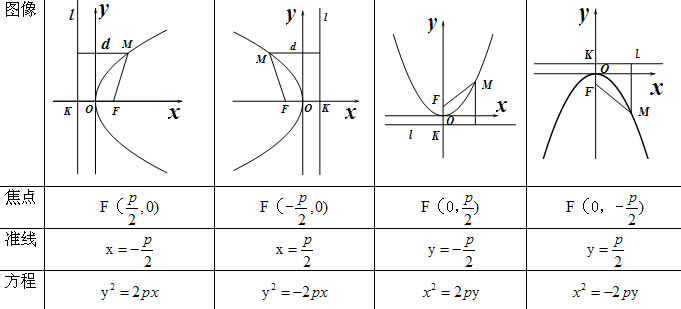
P:焦点到准线的距离. 3. 问题探究 问题5:抛物线的标准方程有哪些不同的形式?请探究后填写下表. 具体要求:以顶点在原点,焦点在x轴正半轴上的抛物线的标准方程为基础,分别写出开口向左、向上、向下,顶点在原点,焦点在坐标轴上的抛物线的标准方程,不要求写过程,学生先独立思考,再小组合作交流,完成下列表格。 | 教材只给出了一种建系方式,但学生在建系时可能不只一种.为了体现学生的自主地位,这里先让学生建系,教师再汇总学生的结果,并用投影仪展示. 通过问题4,让学生分工求出三种建系下的方程,为标准方程的理解奠定基础。 部分学生在推导方程时存在困难,故给出提示. 问题5是教材的探究,目的是让学生认识到抛物线的标准方程一共四种形式,加深学生对抛物线标准方程的理解. 大部分学生解决问题5所用的方法都是图像变换法。老师可以从代数方程的角度加以解释,予与补充。 |
|
抛物线的标准方程是指顶点放在坐标原点,焦点放在坐标轴的抛物线的方程,一共有四种形式。 问题6:能否将问题5的表格归纳一下,以便快速准确的写出抛物线的方程、焦点、准线,并且画出简图。 1.定轴定开口。对称轴为(方程中一次项所对应的)坐标轴;x带平方,开口朝上(一次项系数为+)下(一次项系数为-);y带平方,开口朝左(一次项系数为-)右(一次项系数为+)。 2.定焦点定准线。焦点的非零坐标是一次项系数的1/4;准线与对称轴垂直且垂足与焦点关于原点对称。 4. 例题分析 例1. 求出下列抛物线的和准线方程. (1)已知抛物线的方程,则它的焦点坐标是 , 准线方程是 ; (2)已知抛物线的准线是 ,则它的焦点坐标是 , ,则它的焦点坐标是 , 抛物线方程是 ; (3)已知抛物线的焦点是 ,则它的焦点坐标是 ,抛物线方程是 。 ,则它的焦点坐标是 ,抛物线方程是 。 拓展问题:你能说明二次函数 的图像为什么是抛物线吗?指出它的焦点坐标、准线方程。 的图像为什么是抛物线吗?指出它的焦点坐标、准线方程。 例2:在抛物线 上求一点P,使P到焦点F与到点A(3,2)的距离之和最小。 上求一点P,使P到焦点F与到点A(3,2)的距离之和最小。 变式题:在抛物线 上求一点P, 上求一点P, (1)使P到焦点F与到点A(3,3)的距离之和最小。 (2)使P到y轴与到点A(3,3)的距离之和最小,并求最小值。 | 引导学生观察规律,归纳总结,为后续学习打下基础。 例1的3个小题包含了抛物线标准方程的四种形式.采用小组领任务的形式开展课堂小竞赛。 例1的拓展问题提供了解决课前问题的一种方法。 例2进一步熟练应用抛物线的定义,并且应用“以直代曲”的思想,灵活转化,解决距离之和最小值问题。 |

| 以思维导图的形式展现本节课的收获。培养学生梳理总结、建构知识体系的能力。 |
五、 课后思考和作业 如何用抛物线的定义来证明(1)二次函数 的图像是一条抛物线?(2)二次函数 的图像是一条抛物线?(2)二次函数 的图像是一条抛物线? 的图像是一条抛物线? 作业:课本P73,习题2.4 A组1,2 | 充分利用课本资源,引导学生自主学习课本“探索与发现”的内容(课本P74)。 |
六、 课后延伸 (1) 抛物线型桥梁 课堂通过图片展示赵州桥,多个现代桥梁等抛物线型桥梁。 提出问题:抛物线型拱桥有哪些特点?有哪些优点?在桥梁的设计上利用了抛物线的哪些特征? (2) 抛物面与太阳灶. 提出问题:我们知道一只小灯泡发出的光会分散地射向各方,但把它装在手电筒里,适当调节,能射出一束较强的平行光,这是抛物面的光学性质决定的,人们还用这个原理做出了太阳灶,它利用了抛物线的哪些特征? 对此感兴趣或者学有余力的学生,可以在课后收集相关资料进行学习,并作进一步的探讨。 | 感受抛物线的广泛应用和文化价值,激发学生学习数学的兴趣和研究问题的热情。 |
关键字:












 鲁公网安备 37070502000299号
鲁公网安备 37070502000299号