“函数的零点”教学设计

　　设计思路：

　　目标教学三十年，如何驾轻就熟的开展深度的课堂学习，一直是我们一线教师孜孜以求的目标。本节课的教学设计，旨在解决“如何落实“为应用而学”创新教学情境设计”以及“如何设计和实施“问题导向”的深度学习课堂”两个课堂教学中的常见问题。”

　否　否所以在整节课的情境设计上，我以“女排精神”为主线，从课前引入，到课中例题的设置，再到课尾学习目标的展示，均以此展开，算是一个崭新的尝试。

在问题的设计上，我切实做了一些思考和创新。

　　如：课前问题引入中的“台阶式”设问，在恰到好处的第三问设计学生“触碰不到”的“难题”，引起思维“冲突”，以达到激发求知欲，顺利进入新课的目的。

　　而在课中“捕捉规律”阶段，结合学生熟悉的二次函数图象为推广到一般连续函数设计问题，有明显的整合性和开放性，也就达到了预期效果。

课尾的问题设计，既回应了数学主题，又延伸到应用价值，初步尝试了为“应用而学”问题情境创设。

　　设计本节课，恰逢《中国学生发展核心素养》总体框架正式发布。所谓学生发展核心素养，主要指学生应具备的，能够适应终身发展和社会发展需要的必备品格和关键能力。而我们高中数学教学，在其中也起着至关重要的作用。在六大核心素养中，数学学科在“科学精神”方面对学生的影响不言而喻（这点在本节课中也有具体的体现）；除了以上亮点，本节课的教学还尝试在“责任担当”方面进行一下大胆的尝试。

    “函数的零点”教学设计

     泰安一中    石菁

　　一．教学目标：

　　1.能说出函数零点的定义，会求掌函数的零点， 会画三次函数图象。

　　2.经历由二次函数图象与零点的关系推广到一般连续函数的过程，并能利用图象解决简单应用问题，从中体会“函数与方程”、“数形结合”的数学思想方法。

　　3.通过交流合作，养成用数学的眼光发现问题，并用科学的思维方式给予解决的习惯；在学习新知的过程中，既能批判质疑，又能勇于探究，感受数学的应用价值；树立正确的人生观、价值观以及爱国主义情怀。

　　二．教学重点

　　函数零点的概念与求法，作三次函数图象

　　三．教学难点　　　　　　　　　　

　　作三次函数图象、解决简单应用问题

　　四．教学方法

　　自主探究，合作探究

　　五．教学过程

　　（事先准备小奖品（其实为最后学习目标的引出埋下伏笔），鼓励课堂活动踊跃的学生）

　　（一）新课引入

　　1.情景引入（激发学生的好奇心）

　　2.播放中国女排在2016年里约奥运会夺冠的视频，指出女排的夺冠与数学紧密相连。

　　3.问题引入（激发学生求知欲）

　　（二）概念的形成与深化

　　1.实例引入

　　2.函数的零点

　　4.概念深化

　　函数y=f(x)有零点←→ 方程f(x)=0有实数根

　　←→函数y=f(x)的图象与x轴有交点

　　（三）实践与探究

　　1.自主尝试

　　求下列函数的零点：

　　2.总结升华

　　（学生把一般二次函数零点的判定以表格形式给出）

　　3.深入探究（学生自主探究）

　　当二次函数有零点时，请由图象探究：

　　(1)函数在零点两侧的函数值符号是否改变？

　　(2)相邻两个零点之间函数值的符号是否相同？

　　（学生自主完成）对于二次函数而言：

　　(1)当函数图象穿过零点时，函数值变号；  当函数图象遇到零点但不穿过零点时，函数值不变号.

　　(2)相邻两个零点之间的所有函数值保持同号.

　　（师总结）推广：对任意函数，只要函数图象是连续不断的，上述性质同样成立.

　　（四）应用举例

　　1.（学生亲自投影，面对同学讲解做法，教师适当补充）

　　在这4个区间内，取x的一些值，以及零点，列出这个函数的对应值表：

　　在坐标系内，描点连线，作出图象.

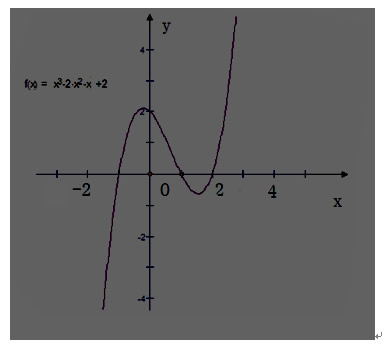
　　【学生总结方法：】

　　求函数y=f(x)零点的方法：求方程f(x)=0的根.

　　（常用：因式分解）

　　画三次函数图象的步骤：

　　（1）求函数的零点，用其将x轴分成几个区间；

　　（2）利用在区间内适当取的x值及零点，得到图象上的一些点；

　　（3）描点连线，得到图象.

　　2.自主尝试

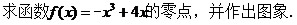
　　(学生黑板板演)

　　【课下研究课题】

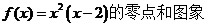
　　3.（回扣课头）

　　例2 研究发现，降低伤痛感的某安全药物（不含违规成分）被运动员服用后，只要体内血液中的药物浓度（即血药浓度）大于0，就能减缓运动员的痛感，使其投入正常的比赛.经测算，某女排运动员使用该药物后的血药浓度y（毫克/升）近似是服药后时间t（小时）的二次函数： 

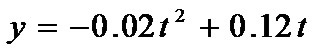
　　假设开始服药时t =0,请计算该运动员服药后几小时内能进行正常的比赛.

　　（五）布置作业

　　书面作业（独立完成）

　　（必做）P 72   练习B；

　　（选做）P75   习题2-4 A组 4，5

　　实践作业（合作完成）

　　寻找生活中可以用函数零点解决的例子，并尝试解决。

　　（六）课堂小结（由学生之间问答引出本节课学习目标）

　　（师）设计了3个有层次的小问题，借学生之间的互动引出本节课学习目标：

　　问题一：本节课你学习了哪些数学知识和方法？

　　问题二：这节课你对那些学习过程印象深刻？（追问：求函数的零点其实就是求什么？解y>0的不等式，其实就是在图象上找什么？）

　　问题三：本节课谈到了里约女排夺冠的历程，你作何感想？

　　（学生回答）得出本节课学习目标：

　　1.能说出函数零点的定义，会求掌函数的零点， 会画三次函数图象。

　　2.经历由二次函数图象与零点的关系推广到一般连续函数的过程，并能利用图象解决简单应用问题，从中体会“函数与方程”、“数形结合”的数学思想方法。

　　3.通过交流合作，养成用科学的思维方式解决问题的习惯，感受数学的应用价值；在学习新知的过程中，既能批判质疑，又能勇于探究，树立正确的人生观、价值观以及爱国主义情怀。

　　（本节课在“歌唱祖国”的歌声中结束）

　　问题一：本节课你学习了哪些数学知识和方法？

　　问题二：这节课你对那些学习过程印象深刻？

　　问题三：本节课谈到了里约女排夺冠的历程，你作何感想？